The earth’s rotation creates a centripetal acceleration field similar to gravity. Fluids in a spinning confined space will accelerate perpendicularly to the axis of rotation. In the thought experiment above, the confined space between the two spheres simulates such a space. Spinning the concentric globes about their axis created a field proportional to the distance from the axis of rotation.
Centripetal force acts on the atmosphere but the curved volume of the atmospheric space reduces the effective force. The effective force is proportional to the cosine of the curved space’s latitude.
To determine the centripetal force at the equator the equation is:
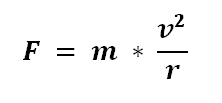
where:
F is centripetal force N,
m is mass (1kg),
v is velocity 465 m/s2, and
r is path radius 6.38 X 106 m.
Earth’s centripetal force at the equator is 0.034 Newtons. However, none of that force affects weather because it is vertical to the earth’s surface instead of tangential to the earth’s surface. We have to calculate the centripetal force tangent to the earth’s surface.
We also have to account for atmospheric buoyancy. The maximum buoyancy of a kilogram of air is only 4.6 % of the air’s mass in the normal range of temperature and humidity values experienced in the United States of America.
To do that we must calculate latitude compensation.
Next page latitude compensation
Back Real World
